Коричневые призмы
Давайте возьмем в руки набор блоков, используемых в Доме ребенка. Конечно, было бы интересно сконструировать ступени Коричневой лестницы с помощью одинаковых призмочек, равных «тонкой» ступеньке, первой в наборе, имеющей в сечении квадрат со стороной 1 см. Сторона квадрата сечения остальных призм возрастает каждый раз на 1 сантиметр, до 10. С этой целью мы приготовили материал, позволяющий осуществить все эти переходы.
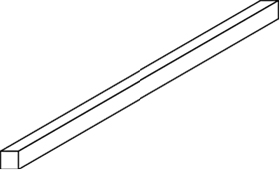
Призма-единица
Сначала мы использовали отдельные призмы. Однако практика заставила объединить их в группы по 2, 3, 4, 5, 6, 7, 8, 9 призм. На разрезе каждой группы линиями обозначены части, из которых состоит группа: они позволяют посчитать призмы. Эти же деления обозначены на прямоугольных сторонах призм. То есть призмы несут в себе указания аналитического характера, позволяющие оценить число их составляющих единиц. Становится видно, что для перехода от первой призмы ко второй нужно добавить три единицы, то есть что вторая призма состоит из 4 тонких призм.
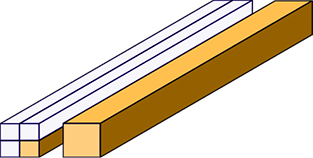
Переход от первой ступени ко второй
После того, как вторая призма составлена из единиц, заменяем ее на цельную призму. На длинных сторонах она несет разметку, означающую отдельные единицы, ее составляющие. К ней присоединяются отдельные призмы и трансформируют ее в призму «3». То есть в такую, сечение которой представляет собой квадрат числа 3.

Переход от второй призмы к третьей
Нам понадобятся две призмочки для каждой из двух смежных сторон, но останется еще пространство вдоль ребра. Оно заполняется еще одной призмой. Чтобы осуществить этот переход, необходимы, следовательно, 5 призм-единиц. И так далее для всех остальных переходов.
Наконец, чтобы перейти от призмы числа 9 к призме числа 10 – последней в серии, – придется покрыть смежные стороны призмы «9», используя две группы по 9 призм в каждой и заполняя пустое пространство вдоль ребра одной-единственной призмой-единицей.
Теперь мы можем заметить, что число призм-единиц, необходимых для нашей цели, точно такое же, какое необходимо для перехода от одного квадрата из бусин к следующему. То есть разница между призмами соответствует разнице между квадратами, и длина призм, будучи постоянной, не привносит в наши расчеты никаких изменений. Даже если длина достигнет двадцати метров, она никак не влияет на расчет соотношений между призмами. При переходе от штанги к штанге (например, от штанги «9» к штанге «10») достаточно добавить только одну – штангу «1».

В случае построения лестницы из призм изменяется квадратное сечение каждой призмы (то есть ее площадь), и, чтобы перейти от предпоследней призмы к последней, нужны 19 единиц. Если теперь сопоставить две крайних призмы всей серии, можно увидеть, что длина призм изменялась от 1 до 10, в то время как площадь ступенек Коричневой лестницы растет от 1 до 100, то есть от 1 до 102.

Расчеты размеров набора призм сводятся, следовательно, к расчету их оснований, то есть к тем, которые можно проделать и на плоских фигурах, так как призмы отличаются одна от другой только своими площадями оснований. Призм 19. Это наибольшее число, необходимое, чтобы перейти от предпоследней ступени к последней. То есть мы вернулись к отдельным призмам, которые попробовали использовать сначала. Иллюстрации в настоящем издании подверглись соответствующим изменениям. Кроме того, нужно заметить, что такое упражнение в первую очередь носит не математический, а сенсорный характер и представлено уже в Доме ребенка.
Отрывок из книги «Психоарифметика», «Народная книга», 2018 Перевод с итальянского Д. Корнилов. Русская редакция Е. Хилтунен Научная редакция А. Колабаев. Рисунки Н. Корочарова, А. Князев.
Статья из журнала «Монтессори-клуб» № 3 (63) 2018












