Возможности классических материалов Монтессори еще далеко не исчерпаны. Есть целый ряд понятий, широко применяемых в современной математике и присутствующих в различных отечественных программах для детских садов и общеобразовательных школ, которые могут быть простым и наглядным образом введены при помощи этих материалов. Например, понятие функции, которое также относится к числу фундаментальных математических понятий. При использовании наглядных конкретных материалов Монтессори, оно вполне доступно пониманию 8-летнего ребенка.
Под воспитанием Мария Монтессори понимала «помощь психическому развитию ребенка с самого рождения». Позднее она трактовала процесс воспитания и образования ребенка более широко, а именно как «помощь в жизни». Ключевым здесь является слово «помощь»: именно оно во многом определяет роль и позицию учителя по отношению к ребенку. При этом материал не является новым вспомогательным средством, которое дано в руки старой активной учительницы, чтобы быть полезным ей при выполнении задачи обучать. Образно говоря, учитель не просто следует «на поводу» у ребенка, а находится рядом с ним, внимательно наблюдая, обгоняя его в случае необходимости на шаг и предоставляя свою помощь и руководство, или же отступая на шаг назад и давая ребенку возможность полностью насладиться самостоятельной деятельностью.

Изучение понятия функции с помощью геометрических тел
Материал
Геометрические тела: треугольная призма, треугольная пирамида, четырехугольная призма, четырехугольная пирамида, куб, конус и цилиндр. Таблички-проекции — равносторонний треугольник, квадрат и круг. Блок А цилиндров-вкладышей.
Прямая цель:знакомство на конкретном материале с понятием функции как соответствия.
Косвенная цель: подготовка к изучению математического анализа.

Презентация
1. Учитель предлагает ребенку попробовать установить взаимно-однозначное соответствие между множеством следующих геометрических тел: треугольная призма, треугольная пирамида, четырехугольная призма, четырехугольная пирамида, куб, конус и цилиндр — и множеством следующих табличек-проекций: равносторонний треугольник, квадрат и круг. Ребенок приходит к выводу, что этого сделать нельзя, причем геометрических тел оказывается больше, чем табличек.
2. Далее учитель просит ребенка поставить каждое геометрическое тело около таблички, одинаковой с его основанием. Ребенок ставит треугольную призму и треугольную пирамиду рядом с табличкой-равносторонним треугольником, четырехугольную призму, четырехугольную пирамиду и куб — рядом с табличкой-квадратом, конус и цилиндр — рядом с табличкой-кругом.

Соответствие между элементами двух множеств X и Y
3. Учитель: «Ты установил соответствие между множеством геометрических тел и множеством табличек. Соответствие между элементами двух множеств X и Y, при котором каждому элементу множества X соответствует единственный элемент множества Y, называется функцией».
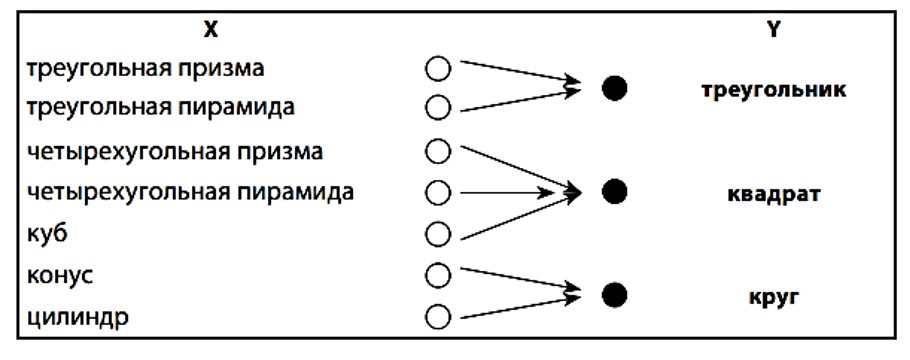
4. Множество геометрических тел обозначают через X, а множество табличек — через Y. В тетради красным карандашом слева друг под другом рисуют столько жирных точек, сколько элементов в множестве X (геометрических тел), а синим карандашом справа друг под другом столько жирных точек, сколько элементов в множестве Y (табличек). Под каждой красной точкой пишут название геометрического тела, а под каждой из трех синих — слово «треугольник», «квадрат» или «круг». Над множеством красных точек пишут букву X, над множеством си них — букву Y. От каждой красной точки рисуют стрелку к соответствующей си ней точке, так что к каждой синей точке оказывается проведено столько стрелок, сколько геометрических тел стоит рядом с соответствующей табличкой.
Учитель: «Сколько стрелок выходит из каждой красной точки? Другими словами, сколько табличек соответствует каждому геометрическому телу?»
Ребенок: «Одна». Учитель: «Значит, это соответствие является функцией!» Материал убирают.
Упражнения 1
Учитель: «Можно сказать, что функция — это правило, по которому каждому элементу одного множества сопоставляется только один элемент второго».
Ребенку предлагают определить, являются ли функциями следующие соответствия между множествами X и Y:
а) X: таблички-проекции — равносторонний треугольник, квадрат и круг, Y: геометрические тела — треугольная призма, треугольная пирамида, четырехугольная призма, четырехугольная пирамида, куб, конус и цилиндр. Соответствие: табличке-проекции сопоставляется тело с одинаковым с ней основанием.
б) X: 10 цилиндров-вкладышей из блока А, Y: отверстия в блоке А. Соответствие: цилиндру-вкладышу сопоставляется подходящее ему отверстие.
в) X: стулья в помещении, Y: столы в помещении. Соответствие: каждому стулу сопоставляется стол.
г) X: однозначные числа, большие нуля, Y: круглые двузначные числа. Соответствие: каждому однозначному числу сопоставляются круглое двузначное число, начинающееся на ту же цифру.
д) X: множество натуральных чисел 1, 2, 3, ... Y: множество четных натуральных чисел 2, 4, 6, ... Соответствие: каждому натуральному числу n сопоставляется число 2n. Ответы необходимо обосновать.

Упражнение 2
Ребенок самостоятельно приводит примеры функций. Контроль ошибок Учитель, контрольные карты с ответами к заданиям.
Возраст: с 8 лет.
Из книги М. Сороковой, Д. Сорокова «МАТЕМАТИКА ПО МЕТОДУ МОНТЕССОРИ для дошкольников и школьников» Изд. «Редкая птица». Москва, 2018











