Публикация из журнала итальянских учителей «Тетради Монтессори» №115, 2012 год перевод Google под редакцией Алексея Колабаева
Действительно ли математика – это так сложно и страшно?
Вот что я узнал из сообщения мисс C. Steenberghe, опытной учительницы школы Монтессори в Амстердаме. Она описала некоторые эпизоды, которые произошли в ее классе. Ученикам была дана презентация вычисления квадратов чисел. Группа детей занималась построениями квадратов чисел на специальном столике с углублениями, расположенными ровными столбцами и рядами.
С помощью нитей и прищепок они могли выкладывать на этом столе безукоризненные квадраты. Если выбрано число 3, то выкладывали 3 строки и 3 столбца расположенных рядом друг с другом, образуя квадрат со стороной 9 единиц. Таким образом, дети визуально воспринимают связь между квадратом числа и площадью квадрата: 3 х 3 = 9 = 32

Из этого образа дети могут составить себе четкое представление о квадрате числа. После неоднократных опытов на этом столике группа детей начала работать в абстрактном расчете квадратов чисел от 1 до 25.
Тогда их внимание переключилось на другой факт: справа налево путем вычитания каждого квадрата из квадрата, который предшествует ему, получается ряд нечетных натуральных чисел.
625 - 576 = 49 576 - 529 = 47
... 9 - 4 = 5 4 - 1 = 3
Повторив тот же процесс для вновь получившегося ряда чисел, можно увидеть, что результат каждого вычитания всегда равен 2.

Если два вычитания оказывались не равны 2, дети пересчитывали их от нуля, чтобы исправить ошибку. Будет ли Ваше любопытство таким же сильным, как у этих детей?
 Удивительно! Дети были поражены этой закономерностью
Удивительно! Дети были поражены этой закономерностью
Но вот в группе детей возникло желание посмотреть, что произойдет с кубом числа. Как говорится в докладе, дети, благодаря предыдущей деятельности с кубом из 1000 золотых бусин, уже были знакомы с третьей степенью и десятичной системой.
Куб числа означает умножить это число три раза:
3 х 3 х 3 = 9 х 3 = 27 = 33
Таким образом, дети начали работать с кубом с большим энтузиазмом и ожиданиями понять неизвестное. Что же произошло? Они начали абстрактно рассчитывать кубы чисел от 1 до 25.
Результаты вычислений дали, конечно, гораздо большие числа, чем с квадратами. Детям потребовалось и больше времени, чтобы выполнить умножение. Но какое это имело значение, ведь в группе было несколько детей, и каждый делал свою часть работы. Вместо двух новых рядов получилась целая серия вычитаний.
Это было открытием само по себе
В результате анализа кубов в последнем ряду было обнаружено число 6. Что же это означает?
1 8 27 64 125 … 15 625
7 19 37 61 …
12 18 24 30 …
6 6 6
«Давайте посмотрим, что происходит с четвертой и пятой степенью. Как мы вычитаем? Какое число получится в результате? Это будет число, кратное 6?» Работа закипела. В этот момент энтузиазм был так велик, что дети полностью погрузились в работу.
«Поток не может быть остановлен, – пишет мисс Steenberghe, – все больше и больше детей, в том числе тех, кто ранее не был увлечен, присоединился к группе».
Опять сделали расчеты для всех чисел от 1 до 25 четвертой степени.
1 16 81 256 625 1296 … 390625
15 65 175 396 671 …
50 110 194 302 …
60 84 108
24 24
Потребовалось уже четыре серии вычетов, чтобы прийти к ряду 24 и 24. Оказалось, что число последнего ряда для степени 2 – это 2. А для степени 3 – это 2 х 3 = 6. А для степени 4 – это 6 х 4 = 24.
«Давайте не будем останавливаться на этой степени, – решили дети, – давайте вычислим все степени до 25 всех чисел от 1 до 25!». Первые результаты расчетов для пятой, шестой, седьмой степени были настолько велики, что они решили прекратить на десятой: данных будет достаточно, чтобы увидеть, если шаблон постоянных рядов повторяется. Так выглядели вычисления для пятой степени: (см. стр. 12) Поддается ли пятый ряд этих вычетов закономерности?
Конечный результат был 24 х 5. Надо ли продолжать?
Мисс Steenberghe отмечает в своем сообщении очень важный момент: «Никогда еще не было сделано так много расчетов, как в эти дни. Никогда детям не требовалось так много внимания, потому что малейшая ошибка могла разрушить регулярность схемы окончательных чисел. Было интересно видеть, что если кто-то допускал ошибки, то обнаруживалось, что полученное число не может занимать любое место в системе. Пересчет начинался снова и снова.
Энтузиазм был велик. Особенно, когда результат доказывал, что они были правы. «После этого упражнение с материалом о возведении всех подряд чисел во вторую степень стало любимой работой».
Как известно, разочарование в предмете математики велико даже среди выпускников. Им трудно представить, что нематериальный объект может иметь более трех измерений.
Например, такое выражение, как (a + b)4, абстрактно. Четвертая степень не может быть представлена в твердой материальной форме. Хотя Эйнштейн показал, что четвертое измерение существует и может быть использовано в расчетах, но, несмотря на это, не может быть представлено физически. Но даже Эйнштейн не пытался показать, как выглядят пятое и шестое измерения. В этом есть некоторая путаница: четвертая, пятая, шестая степени указывают на соответствующие измерения? Ничто не может быть так далеко от истины!
При умножении множитель означает некоторое количество раз, которое надо взять, а не новое измерение. Предположим, что a3 представляет собой куб, стороны которого равны a, чтобы из a3 получить a4, это выражение надо умножить на a, так же как a3 образуется из a2 умножением на a; a3 означает a2 взять столько раз, сколько существует единиц в а.
Материал Монтессори может это показать. Некоторые коробки имеют кубы и призмы, которые представляют a3, a4, a5, a6, a7, a8, a9. Другие модели состоят из различных частей, которые вместе образуют алгебраические формулы (a + b) 4 и (a + b) 5.

Существует модель для представления (a + b + c)3
В первом из этих ящиков степень a3 представлена кубом со стороной 2 см. Расположенные рядом друг с другом два куба образуют призму размером 4 см х 2 см х 2 см, что составляет 24, удлиненная призма.
Две призмы 24 дают плоскую призму 25, если положить две призмы 25, одну на другую, то результат представляет собой куб, стороны которого равны 4 см и значение которого 26 (26 = (22)3 = 43). Если вы повторите этот процесс с вновь образованным кубом, то получается повторение уже полученной модели: удлиненная призма a7, как a4, квадратная низкая призма a8, как a5 и куб a9, как куб a6. Каждые три степени по форме повторяют предыдущие три степени. То есть степени, у которых показатель меняется на число, кратное трем, имеют одинаковую форму. Например, a4 и a7 – это длинная призма.
Чтобы обратить внимание на все части, которые имеют аналогичную форму, для них был выбран один и тот же цвет, явно отличающийся от представленных частей, которые имеют другие формы. Это случай, упомянутый в записях Мисс Steenberghe, стал «любимой работой детей». Они сделали не только расчеты, но и изобразили эти объекты на листе миллиметровой бумаги.
Природа интереса ребенка всегда одинакова, и детям интересно, что бы случилось, если бы вместо основания 2 он взял основание 3. «Точка сознательности», или по-другому «точка удивления», – говорит доктор Монтессори, – это начало интенсивной деятельности, которая ведет к прогрессу».
Таким образом, дети подготовились к изучению куба с ребром 3 см, то есть a = 3. Чтобы a3 преобразовать в a4, его необходимо было умножить на 3. Дети зарисовали каждую деталь в пропорции и были очень впечатлены регулярностью форм и цветов.
Одна группа детей работала со степенями 2 и ушла далеко за рамки a9, в то время как другая группа продолжала работать со степенями 3.

Материализованная идея биномиального и триномиального кубов привели детей к интенсивной деятельности с большой радостью
Если мы возьмем a = 4 см, b = 3 см, c = 2 см, каждый куб с такими размерами раскрашен в свой цвет (например, красного, синего и желтого), биномиальный куб будет состоять из 8 частей, а триномиальный – из 27 частей. Призмы a2b имеют две квадратные грани, окрашенные в красный цвет, как куб, и прямоугольные боковины черного цвета. Так же изготовлены призмы a2c; b2a; c2b, b2c, c2a, а призмы abc полностью черные. Как пишет мисс Steenberghe, они только недавно ввели эти материалы в работу класса. Монтессори-учителю нужно время и практика, чтобы правильно соединить все части биномиального и триномиального куба вместе. Оказалось, что дети могут сделать это быстро и хорошо!

Гармония результата
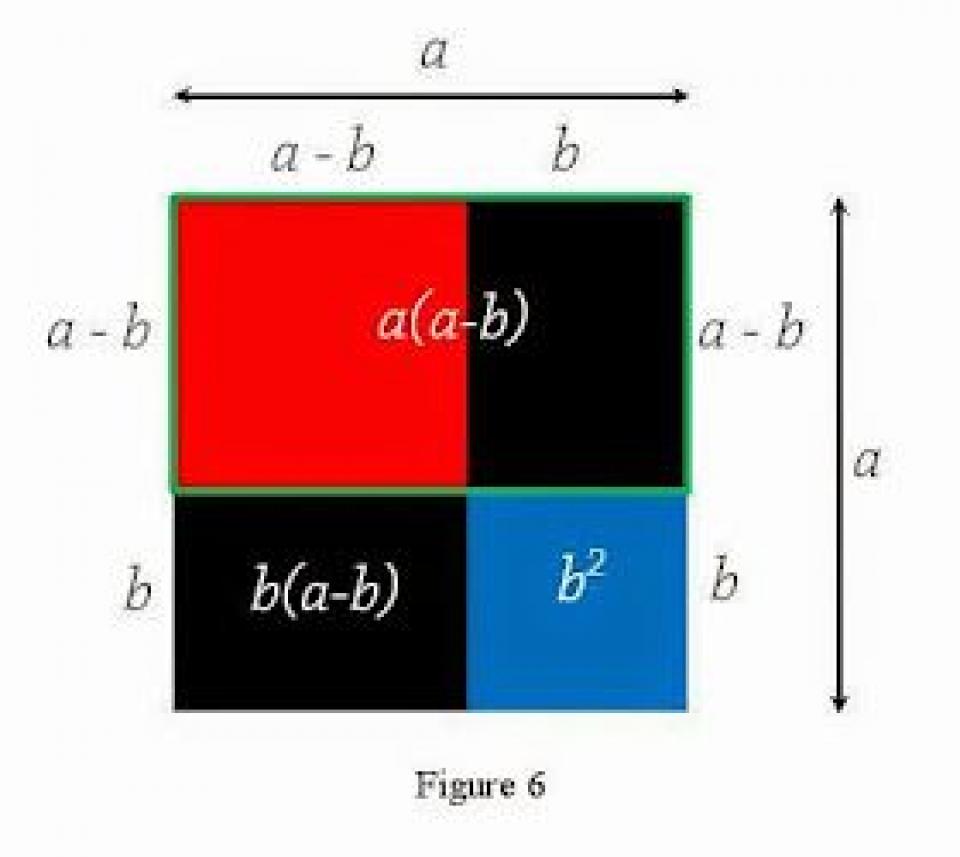
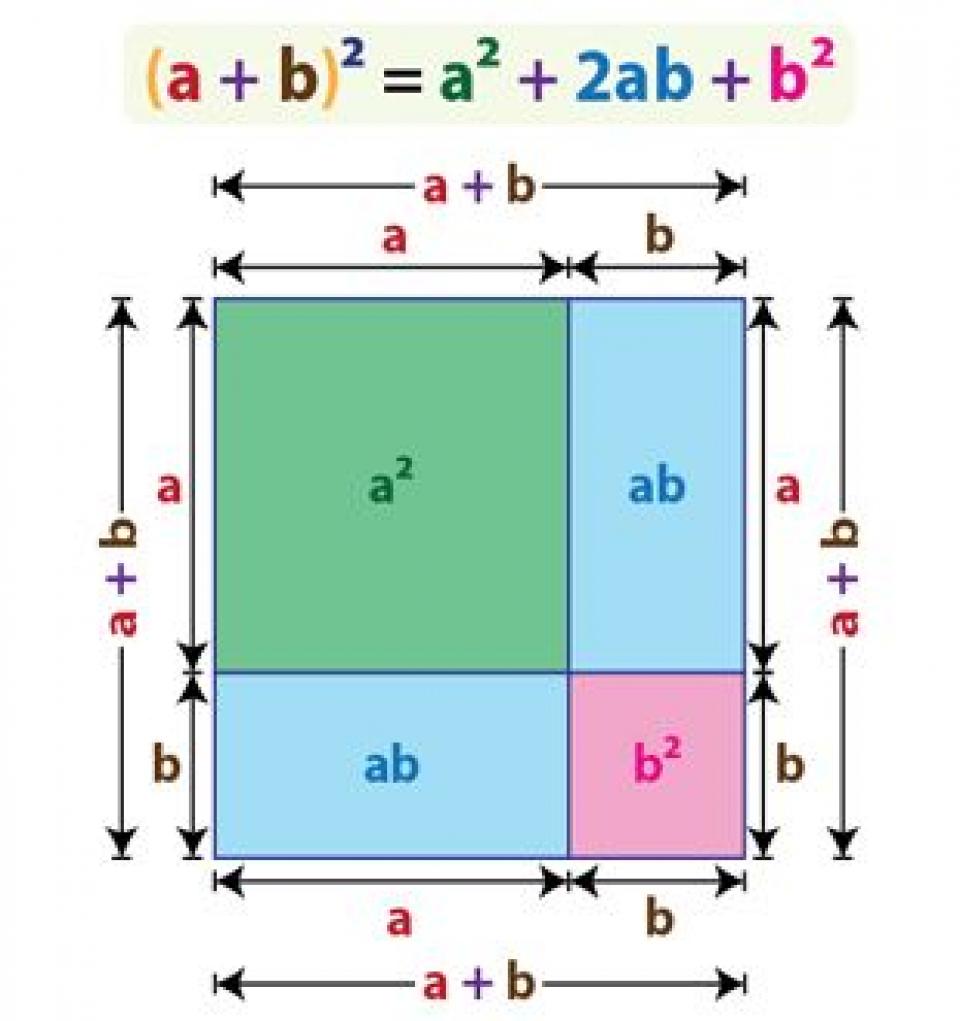
После классификации и расположения рядом равных частей они снова были поражены гармонией полученного результата: (a + b)3 = a3 + a2b + a2b + a2b + b2a + b2a + b2a + b3 = a3 + 3a2b + 3b2a + b3 (a + b + c) 3 = a3 + b3 + c3 + 3a2b + 3a2c + 3b2a + 3b2c + 3c2a + 3c2b + 6abc
Каждая из частей биномиального и триномиального кубов и целиком кубы были правильно нарисованы на миллиметровой бумаге. Особенно большой интерес был вызван сортировкой и записью частей триномиального куба в особенности черной деталью abc.
Далее некоторые дети вдохновились исследовать формулу (a + b + c + d)2, а после возводить ту же формулу в третью, четвертую и пятую степень. И, наконец, логический вывод для тех, кто знает детей. Именно дети разрабатывали формулы квадрата и куба суммы, членами которой были все буквы алфавита.
Для записи и зарисовок различных частей всех описанных упражнений требуется использовать большое количество бумаги. Листы, иллюстрирующие куб суммы всех букв алфавита, когда они были склеены, оказались длиной около десяти метров.
«Пропорционально огромному количеству израсходованной бумаги, – пишет мисс Steenberghe, – было видно и счастье детей, возведенное во вторую или даже третью степень, которое было главным результатом их работы.
Единственные уроки, которые дали монтессори-учителя, состояли в объяснении значения и использования материалов. При необходимости они предлагали детям контроль результатов некоторых их вычислений и давали практические советы по экономии бумаги. В той или иной мере, половина детей класса приняла участие в работе. Интерес был огромным, даже среди тех, кто не был непосредственно вовлечен в работу, а лишь оказался рядом с этим огромным воодушевляющим делом. Преподаватели других классов время от времени заходили, чтобы поинтересоваться, как идет работа и в каких формах.
Каков же был возраст детей? Это была разновозрастная группа детей от 9 до 12 лет. Так оставаться ли предмету математика с такой одиозной репутацией? Очевидно, нет. Тот факт, что дети во всех частях мира реагируют на работу с математическим материалом Монтессори аналогичным образом, является однозначным доказательством утверждения Марии Монтессори: «У человека есть математическое мышление».
Статья из журнала «Монтессори-клуб» № 1 (36) 2013 г.