Слово «игра» подчёркивает интерес, живую и искреннюю радость, которую она способна вызвать у детей. Эти упражнения выходят за школьные рамки, их можно выполнять дома, в качестве полезного и одновременно приятного детям и их друзьям времяпрепровождения. М. Монтессори
Игровое поле представляет собой доску, покрытую квадратами трёх различных иерархических цветов, причём квадраты расположены в виде диагональных полос. Всё это напоминает доску для игры в шахматы.
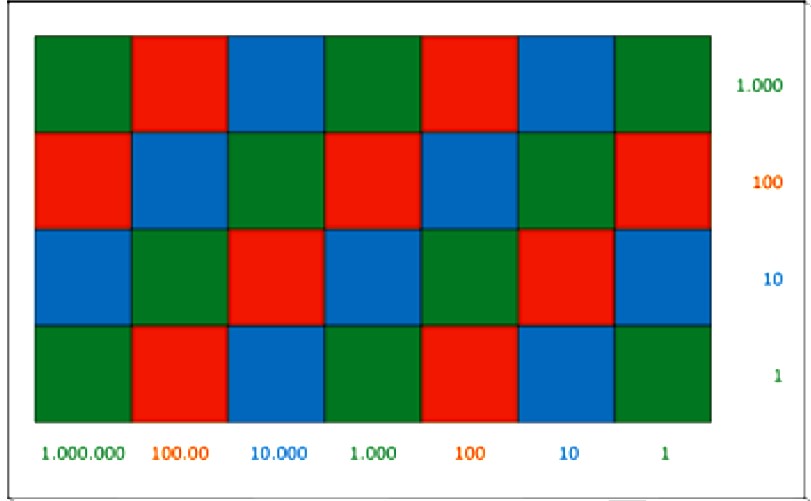
"Шахматная доска"
Материал
Перед нами доска прямоугольной формы со сторонами из семи и четырёх квадратов. Сторона каждого квадрата равна семи сантиметрам, чтобы на нём поместилось синее веретено из девяти бусин (самое длинное из тех, что используются в игре). Вдоль нижней части доски под каждым из семи квадратов соответствующими иерархическими цветами написаны числа: 1, 10, 100, 1000 и так далее до 1 000 000. То же самое с правой стороны доски снизу вверх: 1, …, 1000.
Таким образом, один и тот же квадрат соответствует простым единицам с каждой стороны. Клетки умножаемого расположены горизонтально, а клетки множителя – вертикально.
Чтобы сформировать пример, мы располагаем на доске соответственно клеткам иерархических цветов оба сомножителя с помощью маленьких карточек с числами от 1 до 9, напечатанных на белом фоне для умножаемого и на сером – для множителя. Коробка с большим количеством стержней с цветными бусинами от 1 до 9 служит для обозначения произведений.
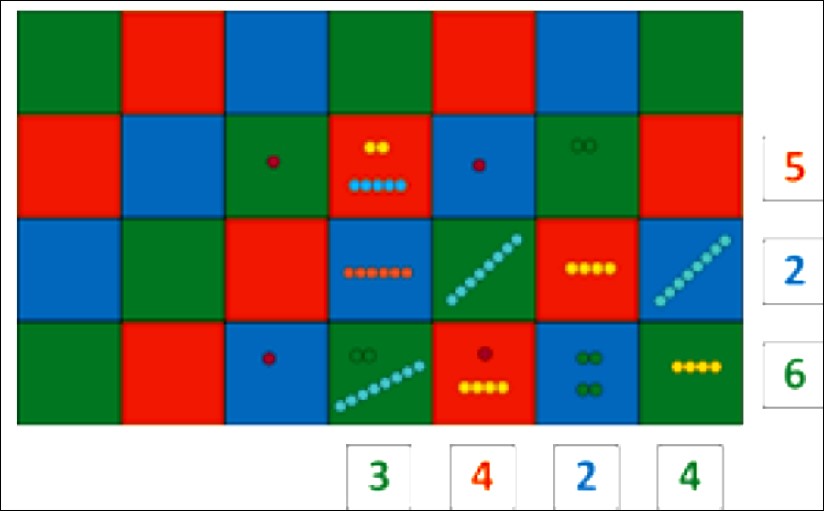
3424 х 526
Различные значения стержней
Прежде, чем начать умножение, ребёнок должен разобраться, что стержни, будучи помещенными в разные квадраты, начинают обладать различным значением. Так, стержень 3, например (абсолютное значение), означает 3 тысячи (относительное значение), когда находится в одном из четырёх зелёных квадратов, соответствующих единицам тысяч, или трём миллиардам, когда занимает единственный зелёный квадрат с таким значением. Десятичное значение каждого веретена изменяется с изменением его положения на «игровом поле» шахматной доски.
Допустим, нам надо умножить 3424 на 526 .
В первую очередь располагаем на поле карточки с нужными цифрами (это сомножители). Затем, начиная с единиц, умножаем каждую цифру умножаемого на каждую цифру множителя и занимаем столько строчек таблицы, сколько записано цифр множителя.
В итоге всех этих многочисленных умножений мы видим, что многие квадраты таблицы заняты группами цветных стержней. Для получения произведения (и это вторая часть упражнения) необходимо сгруппировать все стержни с равным относительным значением, опуская их по диагонали в направлении стрелок, пока они не займут нижнюю строчку таблицы.
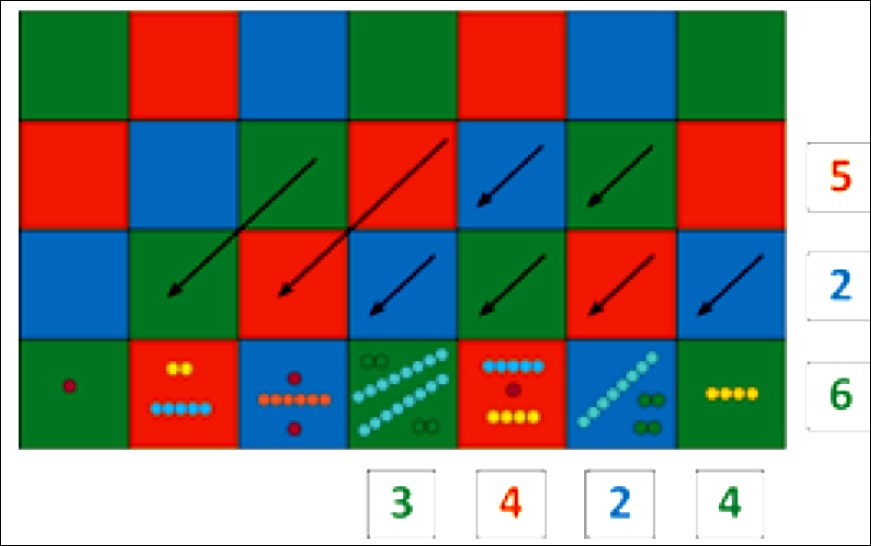Стекание промежуточных произведений
В этот момент мы начинаем подсчитывать бусины на стержнях
Когда сумма достигает 10 (например, на квадрате простых единиц: (8 + 2) + 2 = 10, то есть 1 десяток и 2 единицы), мы заменяем её одной бусиной, которая переходит на соседний левый квадрат. Так происходит каждый раз, когда мы подсчитываем бусины в квадрате, каково бы ни было его иерархическое значение.
Наконец, число бусин в квадрате уже не достигает десятка. Тогда они объединяются и формируют стержень, который, будучи не больше девяти, остаётся в этом же квадрате.
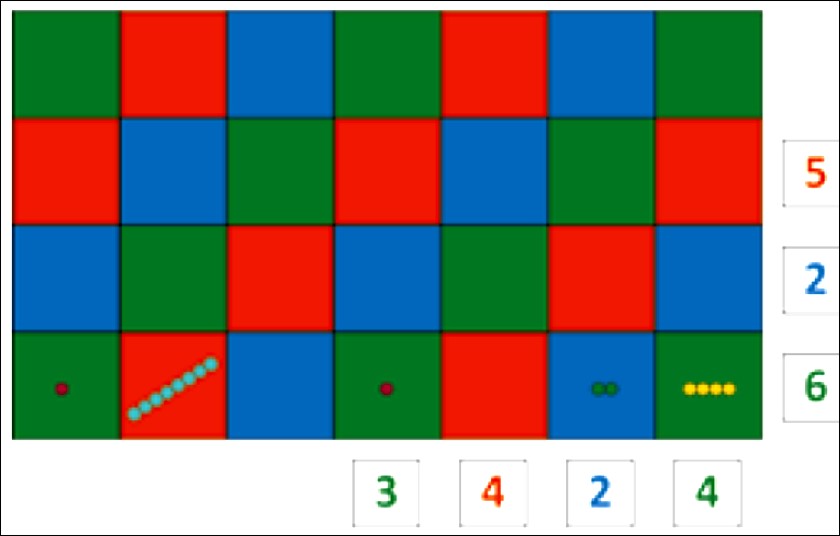
Конечное произведение равно 1 801 024
Полученное число походит на выигравшего игрока
Правила, которые регулируют всю эту деятельность, превращают её в игру на шахматной доске. Полученное число походит на выигравшего игрока.
В игре на шахматной доске мы выражаем умножение геометрически, и это приводит нас к наблюдению, что значения чисел располагаются по диагонали: в угловом квадрате – простые единицы, затем по диагонали сразу слева находятся квадраты десятков, затем – сотен и так далее. Два синих квадрата десятков соответствуют: один – произведению десятков умножаемого на единицы множителя, а другой – произведению единиц умножаемого на десятки множителя. В обоих случаях имеем продукт умножения единиц на десятки.
Три красных квадрата, расположенных вдоль следующей диагонали, соответствуют умножению: сотен на единицы, десятков на десятки, единиц на сотни.
По этой причине достигать суммы, составляющей конечный результат, надо путём группировки стержней, расположенных на квадратах по диагонали, а не по горизонтали или по вертикали.
Цитата из книги М. Монтессори "Психоарифметика". Изд. "Народная книга", 2018.
Видеоролик http://www.youtube.com/@Montessorium
