Необходимо проанализировать каждую трудность ребенка
«Необходимо проанализировать каждую трудность ребенка, рассмотрев её отдельно с помощью конкретного материала; можно сказать, следует «материализовать абстракции», которые для ребёнка не суть недостижимы, к ним нужно только перекинуть мостик из материала.
…В деятельности с математическим материалом ребёнок демонстрирует нам свое понимание, и это лишь первая ступень его длительной и повторяющейся высшей психической деятельности». «Маленького архитектора собственного образования можно сравнить с плотником в его мастерской. Однако понемногу мы замечаем, что он всё чаще переходит в область чистой абстракции, воспринимая алгебраические формулы как проводников в осуществлении сложных арифметических расчётов по извлечению кубических корней. И всё это с бодрой уверенностью человека, устремлённого в бесконечность». Мария Монтессори «Психоарифметика», 1934 год

"Запоминание" таблицы сложения. Змейка
Упражнение, цель которого заключается в тренировке почти механического добавления единиц при счёте, что необходимо для введения устного счёта. Оно выполняется с помощью бусин, представляющих собой числовые группы меньше десятка: 1, 2, 3, 4, 5, 6, 7, 8, 9. Бусины нанизаны на металлические стерженьки, и каждая группа окрашена в свой особый цвет.
Для этого упражнения нам понадобится определённое количество стерженьков с бусинами. Какое число представляет каждый из них, можно узнать, подсчитав бусины на стерженьке. Постепенно распознать количество бусин поможет их цвет: он экономит силы и позволяет не считать каждый раз число бусин. Так каждый стерженек, благодаря своему характерному цвету, с первого взгляда указывает на число. Количество стерженьков представляет не что иное, как группу единиц от 1 до 9.
В начале упражнения случайное количество цветных стерженьков располагается в одну линию. Их можно раскладывать или на столе, или на полу. Именно потому, что цепочка не слишком длинна, получившаяся линия не прямая, а извилистая и напоминает змею.


Начинается пересчет бусин
Как только мы дошли до десяти, так убираем цветные стерженьки «змеи» и заменяем их стерженьком-десятком. Счет бусин продолжается, начиная с десятка, пока их снова не образуется 10. И снова мы заменяем их стерженьком-десятком из золочёных бусин. Так продолжаем, пока не закончится пересчёт бусин змейки. Итак, мы присутствовали при трансформации: золотые стержни мало-помалу поглотили всю нашу многоцветную змейку и стерженьки одинаковой длины постепенно заняли место разноцветных стерженьков разной длины.
В этом случае счёт служил для того, чтобы трансформировать меньшие количества в десятки, составляющие основу десятичной системы. Кроме того, это упражнение даёт возможность попрактиковаться в простом сложении в пределах десятка, поскольку оно начинается каждый раз сначала, и стерженьки-десятки, оставшиеся позади, уже не принимаются во внимание.
Таким образом, происходит постоянное повторение одной и той же деятельности, в результате которой операция сложения чисел меньше десяти становится для ребёнка быстрой, автоматической и простой. Во всяком случае, запоминание происходит в процессе большой работы по пересчёту единиц, в ходе которой приходится снова и снова проверять границы десятков.
Такая работа заставляет задумываться и производить довольно много простых операций вычитания, с тем чтобы одновременно осуществлять сложение и вычислять количество, превышающее десять, после того как десяток уже сформировался.
Упражнение может принимать самые разнообразные формы
Благодаря этой особенности упражнение может принимать самые разнообразные формы, ведь сочетания чисел, заменяемых потом на десятки по ходу формирования змейки, могут быть самыми разными. Опишем теперь более детально, как проходит упражнение.
Допустим, что змейка начинается со следующих стерженьков: 5 + 6. Первая синяя, вторая коричневая: их сумма составляет 11. Мы отделяем два стерженька, заменяя их на золотистый десяток; но остаётся ещё одна бусина, последняя среди коричневых, которая создаёт количество, выражаемое суммой 5 + 6. Иначе говоря, 5 + 6 = 10 + 1. Эта единица относилась к шести – стерженьку, который мы убрали вместе с пятью. Действительно, 6 = 5 + 1, и из этих двух слагаемых или частей 5 служит нам, чтобы образовать 10, а 1 остаётся. 6 - 5 = 1. Число 1, которое осталось, нужно ещё посчитать. Продолжим, и предположим, что следующие стерженьки будут 8 и 6: голубой и коричневый. Сначала необходимо выполнить сложение: 1 + 8 = 9 (1 осталось от предыдущего числа 6). 9 заменить нельзя, так что продолжаем складывать: 9 + 6 = 15 = 10 + 5. Таким образом, мы убираем 1 (старый остаток), 8 и 6, заменяя их десятком и пятёркой. Эта пятёрка – всё, что осталось от 6 после того, как мы заменили его на 1 + 5, чтобы дополнить десяток: (10 + 1) - 6 = 5. [5] Остаток 5 присоединяется к следующим стерженькам по мере продолжения операции.

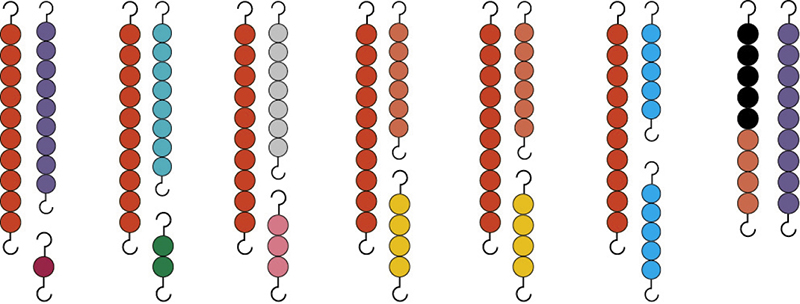
Такие остатки нужно уметь отличать от стерженьков, входящих в состав змейки. Они ярко представляют собой количество, которое нужно считать отдельно (ведь стерженек, посчитанный только частично, не убрать), но о нем нельзя забывать. Существует дополнительный материал, предназначенный специально для того, чтобы обозначить такие остатки и избежать любой возможной путаницы. Он состоит из:
Единица – чёрная бусина;
Двойка – стерженек с двумя чёрными бусинами,
Тройка – стерженек с тремя чёрными бусинами,
Четвёрка – стерженек с четырьмя чёрными бусинами.
Пятёрка – стерженек с пятью чёрными бусинами,
Шестёрка – стерженек с пятью чёрными бусинами и одной белой,
Семёрка – стерженек с пятью чёрными бусинами и двумя белыми,
Восьмёрка – стерженек с пятью чёрными бусинами и тремя белыми,
Девятка – стерженек с пятью чёрными бусинами и четырьмя белыми.
Использование чёрного и белого цвета и особенность их расположения облегчают выбор, потому что отдельные части распознаются с первого взгляда.

Разберём, как проходит операция с большим количеством стерженьков
5 + 6 + 8 + 6 + 2 + 5 + 1 + 4 + 9 + 3 + 4 + 7 + 9.
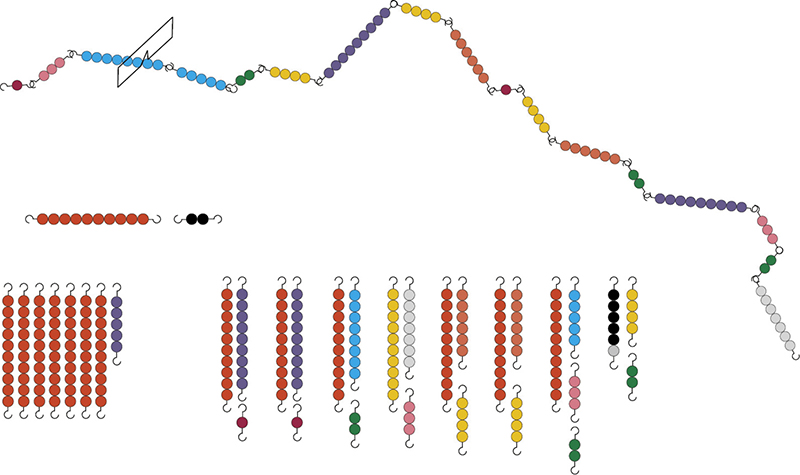
На одном из рисунков показано, как происходит замена стерженьков при образовании десятков.
На линии А мы видим изначально выбранные количества. Постепенно мы заменяем их, и результат этой замены представлен на линии В (тот же рисунок).
Между двумя линиями можно видеть, что оставалось от цветных стерженьков по мере их замены на десятки в ходе операции. Остатки складывались со следующими стерженьками. Результат этой змейки равен 69, то есть 10 + 10 + 10 + 10 + 10 + 10 + 9 (линия В).
Иногда дети выкладывают очень длинные змейки, длиной во многие сотни. По завершении упражнения нужно посчитать стерженьки-десятки, расположив их рядом друг с другом вертикально.
Соединив десять стерженьков, получаем квадрат-сотню, и так до конца. Итог легко достигается именно благодаря различной форме числовых групп десятичной системы (квадрат – сто, линия – десять, и так далее).
Проверку проделанной операции можно осуществить, собрав выбывшие из игры по ходу счёта стерженьки и соединив их по два так, чтобы каждый раз получался десяток (если получится).
Например, если мы складывали 5 + 6 + 8 + 6 + 2 + 5 + 1 + 4 + 9 + 3 + 4 + 7 + 9, то числа можно сгруппировать следующим образом: 9 + 1 8 + 2 7 + 3 6 + 4 6 + 4 5 + 5 9; и убедиться, что каждая группа соответствует одному десятку получившегося результата. В этом случае соответствие полное: 10 + 10 + 10 + 10 + 10 + 10 = 9.
Проверка
Таким образом, происходит изучение всевозможных сочетаний двух чисел, составляющих десяток, с одновременным повторением пройденного при помощи красно-синих штанг.
Упражнение «змейка» требует от ребёнка обратить внимание на сложность счёта десятками. Постоянно повторяясь, эта трудность приучает его к точности, а ряд одинаковых десятков, остающихся позади, успокаивает его. Таким образом, формируется механизм счёта групп единиц в рамках десятичной системы. При использовании обычных методов накопление груза десятков по ходу счёта и групп единиц создаёт впечатление тяжести, и продолжать процесс становится всё труднее и труднее.
В самом деле, когда школьные учителя говорят «этот ребёнок умеет считать до пятидесяти», кажется, что они говорят о тяжести накапливаемых десятков, которую ребёнку, едва начинающему трудный путь, приходится на себя взваливать.
На самом же деле, как бы ни увеличивались числа и ни расширялись области, в которых нужно считать, трудность только одна, и она остаётся всегда той же самой. Она сводится к прыжку от десятка к десятку, о котором мы уже говорили. Он требует активности мышления, хотя и является результатом простых процедур сложения и вычитания, ведущих к образованию десятка и остатка, который необходимо присоединить к следующей группе. В то же время уже накопленные десятки представляют собой мёртвый груз, не годный ни на что, кроме отягощения памяти.

Упражнения со змейками, если их повторять долго, приводят к тому, что работа мысли, связанная с десятком, становится чисто механической. Медленная работа по упорядочению постепенно уступает место умственному механизму. В самом деле, законы, регулирующие интеллектуальную деятельность, работают в направлении экономии работы, препоручая памяти уже накопленные знания, чтобы, в конце концов, появилась возможность посвятить себя новым трудам. Хранилище нашей памяти представляет собой, таким образом, накопление сокровищ по ходу истинного прогресса.
Новые приобретения должны сначала пройти фильтр рационального разума, вместо того, чтобы быть управляемыми непосредственно памятью и её механизмами. Когда должный уровень механистичности счёта при переходе от десятка к десятку будет достигнут, – группы уже накопленных и оставленных позади десятков можно мало-помалу перемещать туда, где они при помощи памяти будут оставаться, пока производятся операции, не представляющие собой ничего трудного.
В упражнении со змейкой эти два вида работы отделены друг от друга. Это позволяет работать быстро и без устали, добиваясь хороших результатов. Накопленные десятки можно с удовольствием подсчитать отдельно, это простая работа после всех уже преодолённых трудностей. Это как подсчитывать накопленные богатства после всех трудов, связанных с их накоплением.
Цитата из книги Марии Монтессори «Психоарифметика». Перевод с итальянского языка на русский Дмитрия Корнилова, русская редакция Елены Хилтунен. Издательство «Народная книга», 2018 Иллюстрации Натальи Корочаровой.
Статья из журнала «Монтессори-клуб» № 5 (60) 2017











