210 отдельных листов с цветными иллюстрациями и чертежами
Эти книги, написанные и отредактированные Ю. Фаусек в контексте нашей социокультурной обстановки, при глубоком отношении к монтессори-педагогике, безусловно, важно прочитать любому российскому Монтессори-педагогу. Наиболее интересная работа Ю. Фаусек о школе вышла пятитысячным тиражом в 1930 году под названием «Школьный дидактический материал Монтессори в обработке Ю.И. Фаусек». Она включала 210 отдельных листов с цветными иллюстрациями и чертежами и 32 страницы отдельно сброшюрованного текста.
В работе подробно описаны коллекции языкового и математического материала Монтессори, большую часть которого Юлия Ивановна изготовила сама. В 1936 году у нее появилась возможность экспериментальной работы с этим материалом в начальных классах 21-й Ленинградской школы, где она в это время работала заведующей методическим кабинетом.
«Работа с материалом, – пишет Юлия Ивановна, – разбита на элементы, представляющие сами по себе вполне самостоятельные, законченные и отвечающие интересам детей упражнения. Но эти элементы, из которых потом в сознании ребенка складывается стройное и ясное целое, не являются строго ограниченными той дисциплиной, к которой они относятся; многие из них переплетаются и с другими дисциплинами. Это делается еще очевиднее, если проследить весь школьный материал Монтессори, тем более, что дети Монтессори не обязываются ни к каким общим классным (так называемым в настоящее время фронтальным) урокам, а предоставлены свободному выбору занятий, на которых мы можем наблюдать, как они сами связывают между собой различные предметы в зависимости от интереса и наклонностей».
.jpg)
В логике М. Монтессори предмет математики рассматривается как способ овладения миром с помощью познавательного действия
В начальную школу Монтессори дети приходят, уже имея первое представление о числе, количествах и цифрах, их изображающих. Упражнения с первыми группами математических материалов в детском саду Монтессори помогли им перевести эти представления в понимание процесса счисления. В начальной школе им предстоит развернуть этот процесс до культурного навыка.

Плоские геометрические вкладки
Первым геометрическим материалом у детей Монтессори являются 32 плоские геометрические вкладки, при помощи которых дети упражняют руку и глаз для письма и попутно знакомятся со многими фигурами планиметрии: квадрат, прямоугольник, треугольник, многоугольник, круг, эллипс и др. Дети, бывшие в детском саду Монтессори, знакомились с ними еще раньше при упражнении органов чувств.
Если в распоряжении детей имеются карточки третьей серии, на которых геометрические фигуры изображены в виде чертежей, дети научаются распознавать их как фигуры, очерченные простыми линиями (абстракция).

Материал для изучения круга
Следующий материал, представленный Монтессори для элементарных классов, является собственно продолжением первого, т. е. ящика со вкладками и карточек. В школах Монтессори за границей этот материал сделан из оцинкованного железа, в нашей же практике (за невозможностью иметь железный) мы пользовались материалом, сделанным из дерева.
У Монтессори геометрический материал очень богатый и разнообразный; в моей же практике я располагала лишь небольшой его частью, во-первых, потому, что достать его или сделать было очень трудно, а во-вторых, потому, что дети, с которыми мы проводили работу со школьным материалом Монтессори все четыре года нашей работы, были не старше 9 лет. Я буду описывать лишь тот материал, который был в нашей практике.
Первая серия вкладок (для изучения дробей)
На одном деревянном лотке (66 х 27 см) помещаются десять рамок. Каждая рамка с круглым дном в 10 см в диаметре представляет собою квадрат, сторона которого равна 13 см. В первую рамку вставлен целый круг (10 см в диаметре), во вторую — круг, разделенный по диаметру на две равные части, в третью – радиусами на три, и т.д. до 10 равных частей (секторов).
В каждый сектор круга вставлена маленькая высокая кнопка (из дерева) для того, чтобы можно было вынимать их со дна рамки. Этот материал дает возможность бесчисленных комбинаций, которые все являются чистыми упражнениями в счете с дробями.
Так, например, ребенок вынимает из рамки целый круг, который мы обозначаем 1, и вместо него вставляет один сектор, равный половине круга, один равный одной четверти и два сектора по одной восьмой, у него получится опять целый круг, составленный из четырех частей.
В результате получится запись: 1/2+1/4 + 1/(8 )+1/8=1/2+ 1/(4)+2/8= 1/2+ 1/4+1/4= (1)/2+1/2= 2/2 = 1. Ребенок, вставляя вместо 1/2 2/4, конкретно видит, что 1/2 = 2/4, то же самое 2/8 = 1/4 , а 2/2 = 1.
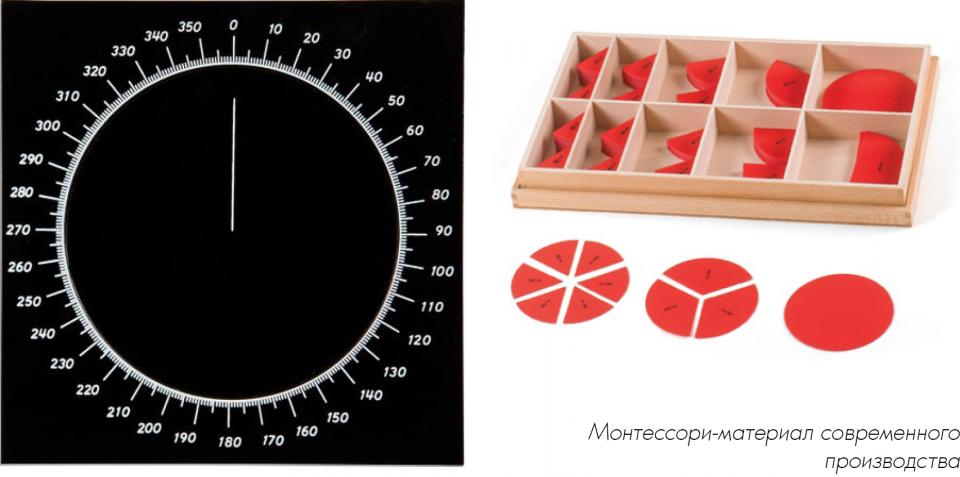
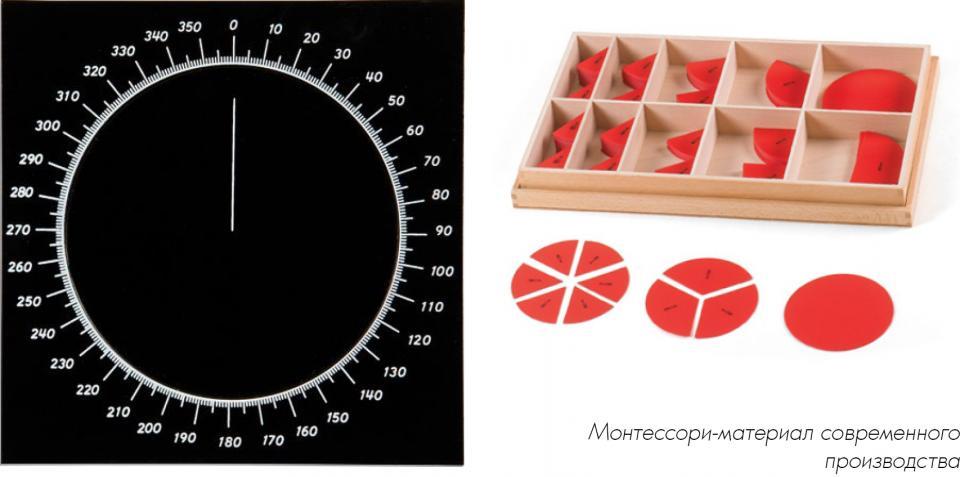
На этом же материале дети учатся также изучать углы каждой части круга и отсчитывать градусы. Для этой цели служит карточка (12 х 12), вырезанная из черного бристольского картона, на которую наклеен белый круг диаметром в 11 см, вырезанный из белой плотной бумаги.
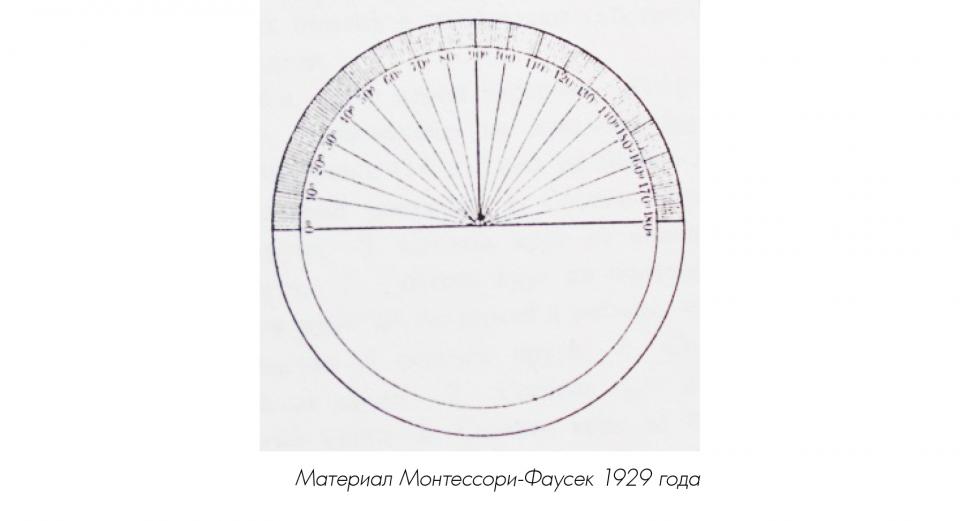
На этом круге радиусом в 5 см начерчено полукружие, разделенное на 18 секторов, которые переходят через окружность. Каждый сектор содержит 10 градусов, отмеченных делениями (градусами). Градусы отмечены цифрами от 0 до 180. Точки 0° и 180° соединены жирной линией, обозначающей диаметр, и на нем точкой и черточкой вниз ясно обозначен центр, для того чтобы ребенок знал, куда приложить угол изменяемого сектора. Также жирной линией обозначен и радиус, соединяющий центр с точкой 90°.
Ребенок вынимает из вкладки часть круга (сектор) и накладывает его на картонный круг так, чтобы вершина угла совпадала с центром, а одна из сторон – с радиусом от центра до точки 0°.
Таким образом дети могут измерить все части круга от 1/2 до 1/10 и из этих упражнений они узнают (накладывая на пластинку целый круг), что круг содержит 360°, половина круга – 180° и что прямой угол равен 90°.
При измерениях у детей получаются следующие записи: 1/2 круга = 180°,то есть 360° : 2=180° 1/3 круга = 120°,то есть 360° : 3=120° 1/4 круга = 90°,то есть 360° : 4= 90° 1/5 круга = 72°,то есть 360° : 5 =72° 1/6 круга = 60°,то есть 360° : 6= 60° 1/7 круга = 51°,то есть 360° : 7= 51° 1/8 круга = 45°,то есть 360° : 8= 45° 1/9 круга = 40°,то есть 360 : 9=40° 1/10 круга = 36°,то есть 360 : 10=36°
Таким образом дети научаются писать дроби и производить с ними всякие действия чисто опытным (исследовательским) путем вплоть до сокращения и приведения дробей к одному знаменателю и исключению целого числа из неправильной дроби.
Так, например, у ребенка сложен круг из 5/10 , 1/(4) и 2/8 , он пишет 5/10 + 1/(4) + 1/4= 1/2 + 1/2 = 2/2 = 1 (сокращение дробей), или у него составлен круг из 1/2, 1/4 и 2/8 . Он записывает 1/2 + 1/4 + 2/8 = 4/8 + 2/8 + 2/8 = 4/8 + 4/8 = 8/8 = 1 (приведение дробей к одному знаменателю).
Если ребенок берет перемешанные части круга и захочет составить один целый круг, то у него могут получиться различные комбинации. Например, перед ним лежат два сектора по 1/3 круга и пять секторов по 1/9 круга. Ребенок выкладывает секторы в пустую ячейку целого круга, начиная с бОльших (1/3), и у него укладываются два сектора по 1/3 и три по 1/9 и два сектора по 1/9 остаются. Следовательно, во всех этих секторах заключается целый круг (1) и еще 2/9 круга. Это можно записать так: 1/3 + 1/3 + 1/9 + 1/9+ 1/9 + 1/9 + 1/9 = 2/3 + 5/9 = 6/9 + 5/9 = 11/9 = 12/9.
Дети проделывают много собственных опытов и изобретают собственные, часто весьма сложные, задачи.

Задачи на дроби
Две серии карточек. Первая серия содержит задачи, относящиеся ко вкладкам (кругу, разделенному на части). Карточки (14х3 см) из белого бристольского картона с цветной каемкой:
1. Составь круг из половины и четвертей круга.
2. Составь круг из половины, четвертей и восьмых круга.
3. Составь круг из половины и восьмых круга.
4. Составь круг из четвертей и восьмых круга.
5. Составь круг из половины и шестых круга.
6. Составь круг из половины и десятых круга.
7. Составь круг из четвертей, восьмых и десятых круга.
8. Составь круг из третей и шестых круга.
9. Составь круг из третей и девятых круга.
10. Составь круг из третей, шестых и девятых круга.
11. Составь круг из пятых и десятых круга.
12. Составь круг из четвертей и десятых.
13. Составь круг из восьмых и десятых. Все эти карточки лежат в отдельной коробочке с надписью: «Задачи на дроби № 1».
Вторая серия — карточки (12 х 3 см) из цветного бристольского картона:
1 (розовая). Возьми 1/2 от 16 кубиков.
2 (голубая). Возьми 1/4 от 20 кубиков.
3 (зеленая). Возьми 1/8 от 24 кубиков.
4 (красная). Возьми 2/3 от 15 кубиков.
5 (желтая). Возьми 3/5 от 30 кубиков.
6 (оранжевая). Возьми 1/6 от 36 кубиков.
7 (серая). Возьми 2/7 от 14 кубиков.
8 (коричневая). Возьми 2/9 от 27 кубиков.
9 (белая). Возьми 1/10 от 40 кубиков".
Все карточки лежат в коробочке с надписью "Задачи на дроби № 2".
Превращение простых дробей в десятичные
Для решения этих задач нужны мелкие предметы: кубики, пуговки, бобы (всегда однородные). Записи могут быть двух родов. Например, в задаче 4-й (2/3 от 15 кубиков) 15 : 3 = 5; 5 х 2= 10 или 2х15 = 30; 30:3=10.
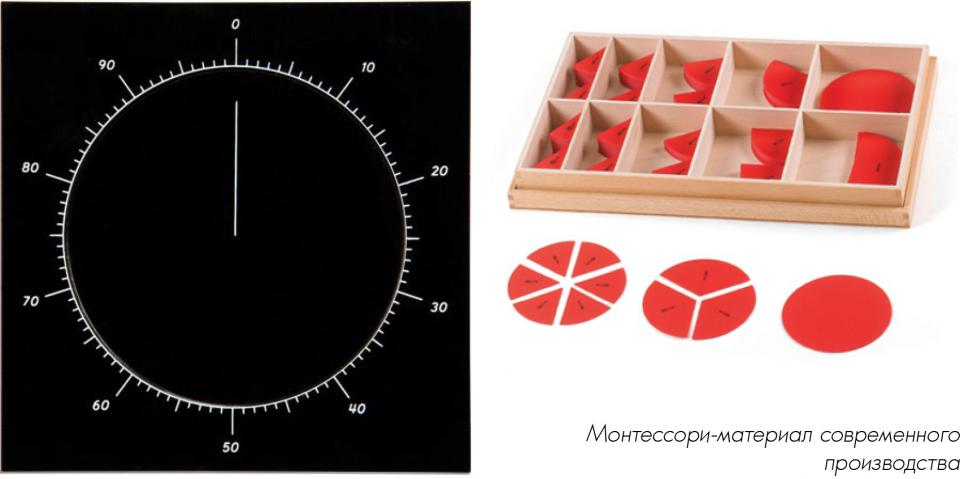
Для превращения простых дробей в десятичные к деревянным вкладкам (кругам, разделенным на части) прилагается картонная карточка (12х12), вырезанная из белого бристольского картона. На ней начерчен круг (11 см в диаметре). В этом круге радиусом в 5 см начерчен другой круг и пространство (дуга) между двумя окружностями 1/2 см шириною) разделено на 10 равных частей, а каждая десятая еще на 10 частей. На этих мелких делениях черточки пяти немного длиннее других. Все большие деления отделены одно от другого жирной черточкой и помечены цифрами; 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Знак 100 стоит наверху, и от черточки, его обозначающей, проведен к центру круга радиус. К нему прикладывается одна сторона каждого измеряемого сектора.
Работа с этой карточкой производится следующим образом: ребенок берет один из секторов любого разделенного на равные части круга и прикладывает одну его сторону к радиусу от центра к точке 100 направо так, чтобы вершина угла совпала с центром, и смотрит, на каком делении кончается дуга сектора.
Число делений отвечает сотым долям сектора. Так, если сектор равен 1/4 круга, то его дуга (направо) кончается на 25, следовательно, (1)/4 = 0,25. Если сектор равен 1/5 круга, то его дуга направо кончается на 20, следовательно, 1/5 = 0,20.
Если ребенок наложит на карточку несколько секторов, прикладывая первый одной стороной к радиусу, а другие последовательно к первому, то он получит общую сумму нескольких простых дробей, превращенных в десятичные. Так, например, если у него будет три сектора: в 1/3 круга, в 1/4 и в 1/8, при наложении на круг их дуги кончаются на 70, и все это может быть выражено так: 1/3 + 1/4 + 1/8 = 0,70. Знания, приобретаемые детьми самостоятельно чисто опытным путем, очевидны.
Из книги «Школьный материал Монтессори», «Библиотека педагога», Государственное издательство «Москва-Ленинград», 1929
Статья из журнала «Монтессори-клуб» № 3 (53) 2016