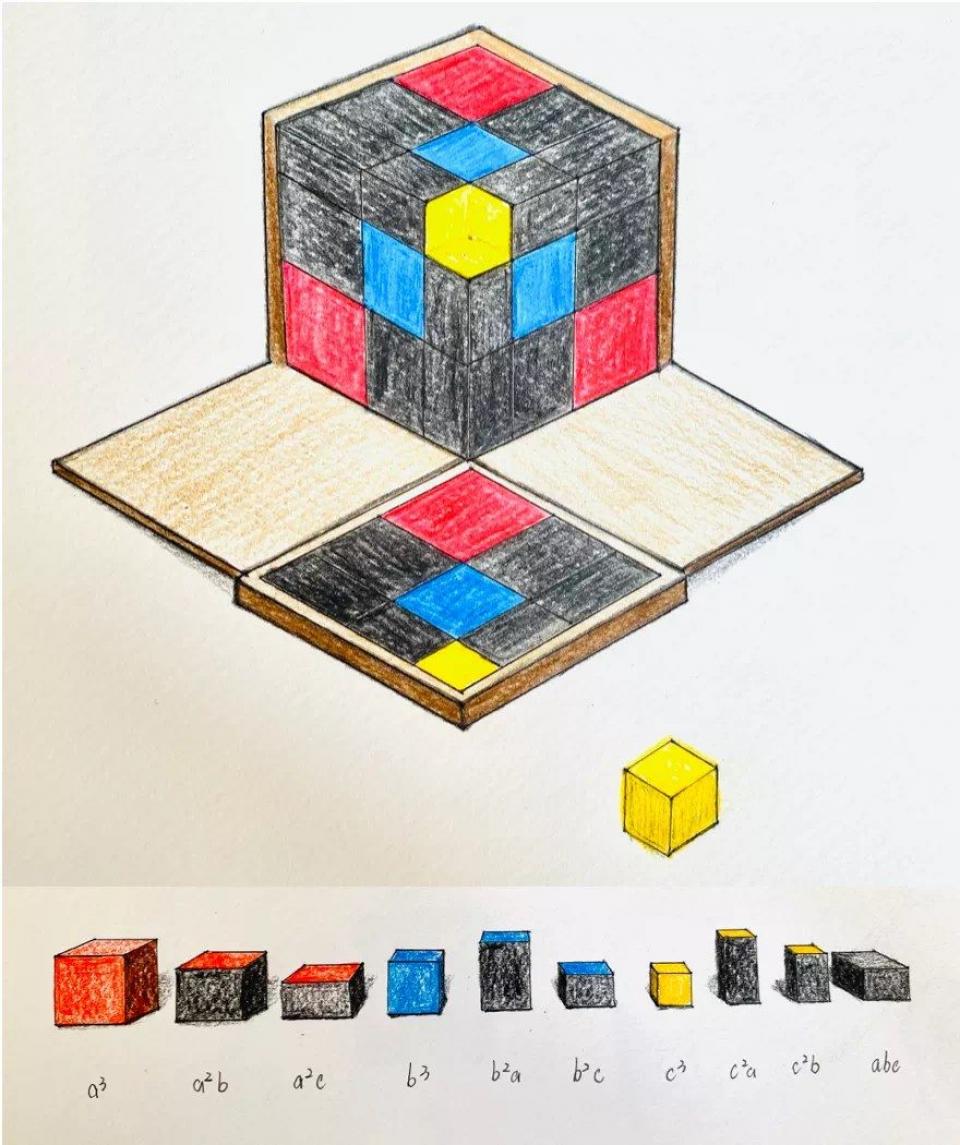
Тактильный опыт и возможность исследовать и экспериментировать с формами и размерами
«...Вместо того, чтобы делать все кубы и строительные детали одинаковыми по размеру, я предложила разрезать большой деревянный куб (длина ребра которого около 10 см) соответственно делению ребер на две неравные части; затем — другой куб соответственно делению ребра на три неравные части.
При отделении частей, полученных при таком подразделении, получились маленькие кубы и прямоугольные призмы различной формы. Это было материальным представлением алгебраических выражений, то есть третьей степени бинома и тринома. Тела с одним и тем же десятичным значением были одного и того же цвета. Так при открывании коробки был виден один единственный предмет. Куб, раскрашенный в разные цвета, отдельные компоненты которого были сложены вместе, но все же разделены на группы.
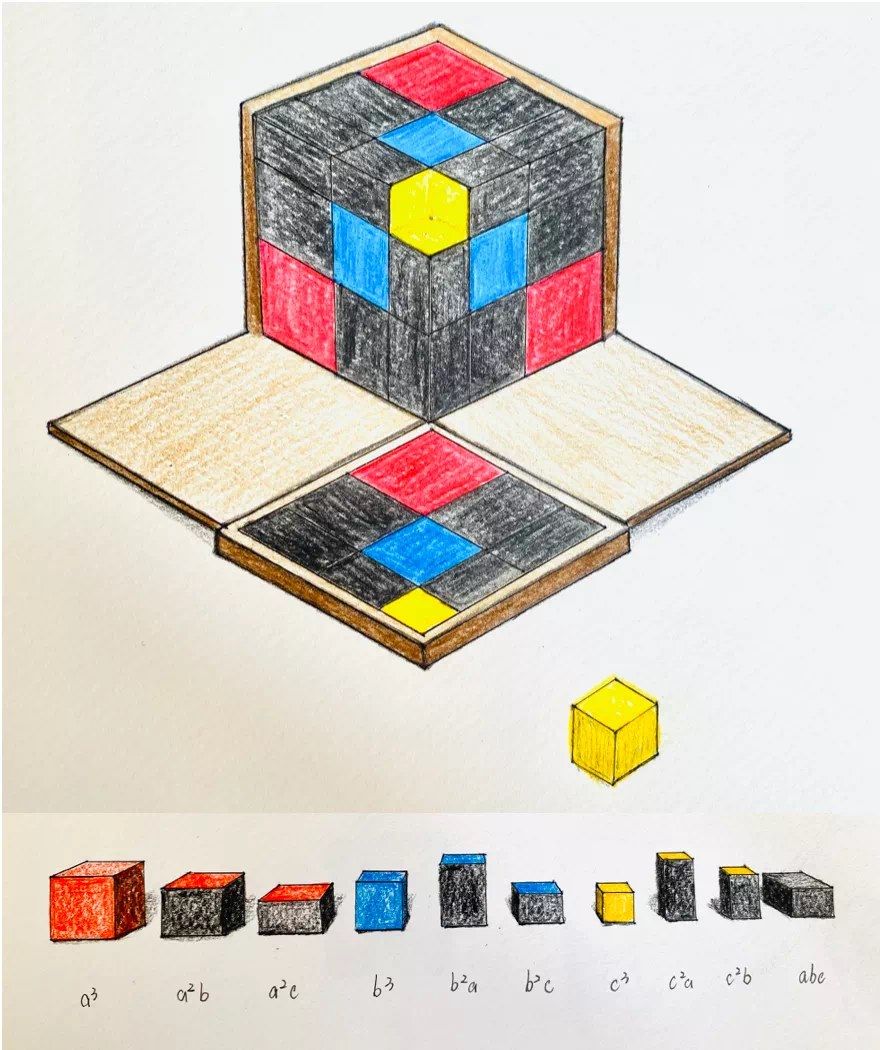
Например, в триноме было 3 куба разного размера различных цветов, такое же количество призм с квадратным основанием одного и того же цвета (предположим, зеленого), 3 другие призмы, обладавшие также квадратным основанием, но других размеров, окрашенные, например, в желтый цвет, еще 3 призмы с квадратным основанием, которые снова отличались от двух других групп и были окрашены, например, синим, и, наконец, 6 совершенно одинаковых призм с прямоугольными основаниями, окрашенные черным. Эти маленькие цветные предметы выглядели притягательно. Здесь речь идет прежде всего о том, чтобы сгруппировать их по цвету, затем различным способом упорядочить...
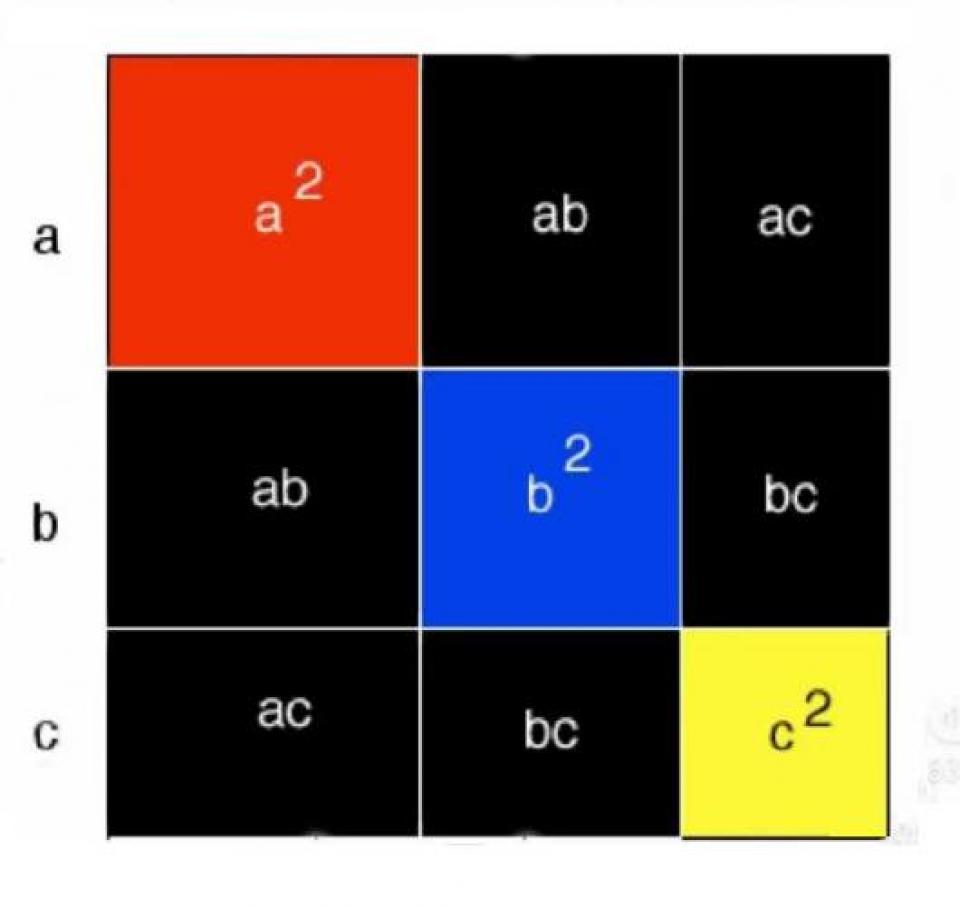
При применении этого материала достигается множество результатов; один из них является расположением членов алгебраической формулы:
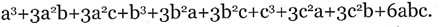
Наконец, кубы кладут в определенном порядке в коробку, и так возникает большой разноцветный куб:
(a+b+c)3
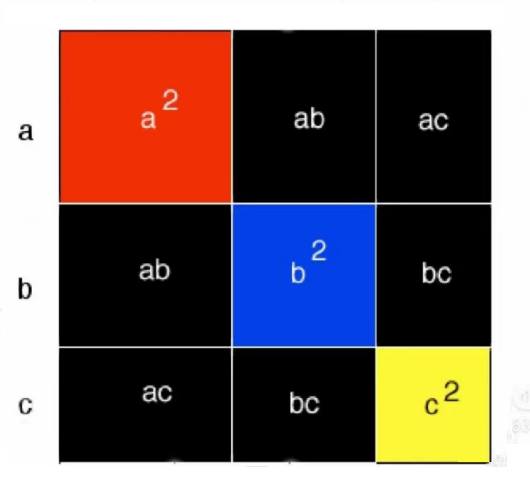
В игре с этим материалом формируется визуальная картина расположения предметов, а поэтому также запоминание их количества и порядка». (Монтессори М. «Психоарифметика»)
Как видим, визуальное, а значит, сенсорное и деятельностное восприятие мира снова работает на развитие мышления. Ребенок собирает биномиальный или триномиальный куб, сравнивая грани призм и кубиков и прикладывая их друг к другу: красную — к красной, синюю — к синей, черную — к черной. Чтобы получился настоящий куб, ему приходится подбирать эти призмочки и кубики еще и по размеру. Он вынужден тщательно анализировать собственные действия, и именно это работает лучше всего на развитие детского мышления.
Цитата из книги Е.А. Хилтунен «Детский сад по системе Монтессори. Методические рекомендации для педагогов» Изд. «Национальное образование», 2015 год.